首页 题解

# Solution

原题

# Point 1 建图

首先是如何建模 AA 的最长上升子序列，可以参考这道题。

简单描述一下，就是对于每一个位置 ii，求出以 AiA_i 结尾的最长上升子序列长度 dpidp_i，此时最长上升子序列长度 lenlen 就是 max⁡{dpi}\max\{dp_i\}。

然后将满足 dpj=dpi+1dp_j=dp_i+1，Aj>AiA_j>A_i，j>ij>i 的 jj 与 ii 相连，对于本题的样例应该最终的图张这样：

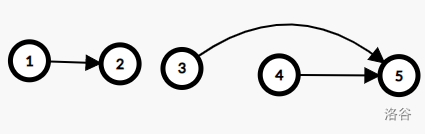
最后将源点 ss 与 dpi=1dp_i=1 的 ii 相连，将 dpi=lendp_i=len 的 ii 与汇点 tt 相连，就能保证每条路跑出来都一定是 最长 的了。

不难想到，如果要使最长上升子序列长度 −1-1，必然要让 s,ts,t 不连通。反证法易得，s,ts,t 连通时必然有一条路径能经过 lenlen 个点。

既然要使 s,ts,t 不连通，其实就是求最小割点。可以考虑拆点，将每个点拆分为 u1,u2u_1,u_2 两部分，连接一条 (u1,u2,wu)(u_1,u_2,w_u) 的边，对于原图中 (u,v)(u,v) 改为 (u2,v1,inf⁡)(u_2,v_1,\inf)，这样就能将最小割点转化为最小割边（即最小割）了。

# Point 2 方案输出

直接将图看成一张网络，现在需要求的就是字典序最小的割边方案。

想想最小割的定义，将点分为两个集合 S,TS,T，割掉总权值最小的一些边使得 S,TS,T 不连通。那么对于一条边 (u,v)(u,v)，它能成为最小割边当前仅当满足下面两个条件：

  1. (u,v)(u,v) 满流。
  2. 残量网络 上不存在 u→vu\to v 的路径。因为在满足第一点的前提下，必然存在 v→uv\to u 的路径，这句话其实就是说 u,vu,v 不在同一个强连通分量里。

运用 最大流最小割定理，可以很容易推出第一点。

对于第二点，如果 u,vu,v 在同一个 SCC 里，那一定可以通过流量调整（匀一点流量）使得 (u,v)(u,v) 不满流，此时就不满足条件了。

最后因为要字典序最小，所以每次选择字典序最小的可行边即可。但是每次选择完这条边后，必须要把这条边带来的影响也删去，即退流。可以直接在残量网络上从 u→su\to s，t→vt\to v 跑两边最大流。也不用担心跑的最大流会不会比 c(u,v)c(u,v) 大，即退流退多了，因为网络流有 反对称性 和 流量平衡 的特点，s→us\to u 最大流了多少，u→su\to s 最大也只能流多少。

具体如何找到这条满流边：因为满流边必定是拆点后的中间边，即 (u1,u2,w)(u_1,u_2,w)，我们可以记录下每个点的 u1u_1，然后按照每个点的 CiC_i 排序，从小到大找每个点，然后判断这个点对应的边是否在最小割上。

# Code

需要 吸氧。

#include <cstdio> 
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#define LL long long
#define F(i, s, e) for(int i=s;i<=e;++i)
#define inf (LL)(1e18)
#define INF (int)(2e9)
#define N 2005
using namespace std;
struct edge { int v; LL f; };
struct node { LL w; int p, id; } nd[N];
vector <edge> E, E_;
vector <int> G[N];
int n, m, s, t, T, cur[N], dep[N], A[N], B[N], C[N], dp[N], len, stk[N], tp;
int add(int u, int v, LL w) {
	E.push_back((edge){v, w});
	E.push_back((edge){u, 0});
	G[u].push_back(E.size()-2);
	G[v].push_back(E.size()-1);
	return E.size()-2;
}
void init() {
	scanf("%d", &n);
	E.clear(); F(i, 0, N-1) G[i].clear();
	F(i, 1, n) stk[i] = dp[i] = 0;
	tp = len = 0;
	F(K, 1, 3) F(i, 1, n) switch(K) {
		case 1: scanf("%d", &A[i]); break;
		case 2: scanf("%d", &B[i]); break;
		case 3: scanf("%d", &C[i]); break;
	}
	s = n*2+1; t = s+1;
	F(i, 1, n) {
		dp[i] = 1;
		F(j, 1, i) if(A[j] < A[i])
			dp[i] = max(dp[i], dp[j]+1);
		len = max(len, dp[i]);
	}
	F(i, 1, n) {
		nd[i].w = C[i]; nd[i].p = add(i, n+i, B[i]); nd[i].id = i;
		if(dp[i] == 1) add(s, i, inf);
		if(dp[i] == len) add(i+n, t, inf);
		F(j, i+1, n) if(dp[j] == dp[i]+1 && A[j] > A[i]) add(i+n, j, inf);
	}
}
bool bfs(int S, int T) {
	F(i, 1, 2*(n+1)) dep[i] = 0; dep[S] = 1;
	queue <int> q; q.push(S);
	while(q.size()) {
		int u = q.front(); q.pop();
		for(int i=0;i<G[u].size();++i) {
			edge& e=E[G[u][i]];
			if(e.f && !dep[e.v]) {
				dep[e.v] = dep[u] + 1;
				q.push(e.v);
			}
		}
	}
	return dep[T];
}
LL dfs(int u, LL in, int T) {
	if(u == T) return in;
	LL flow = 0;
	for(int& i=cur[u];i<G[u].size();++i) {
		edge& e=E[G[u][i]];
		if(e.f && in && dep[e.v] == dep[u]+1) {
			LL d = dfs(e.v, min(in, e.f), T);
			flow += d; E[G[u][i]^1].f += d;
			in -= d; e.f -= d;
		}
	}
	return flow;
}
inline bool cmp(node x, node y) { return x.w < y.w; }
void back(int u, int v) {
	while(bfs(u, s)) {
		F(i, 1, t) cur[i] = 0;
		dfs(u, inf, s);
	}
	while(bfs(t, v)) {
		F(i, 1, t) cur[i] = 0;
		dfs(t, inf, v);
	}
}
void solve() {
	LL mxf = 0;
	while(bfs(s, t)) {
		F(i, 1, t) cur[i] = 0;
		mxf += dfs(s, inf, t);
	}
	sort(nd+1, nd+n+1, cmp);
	F(i, 1, n) {
		int p = nd[i].p; int u = nd[i].id;
		if(E[p].f == 0 && !bfs(u, u+n)) {
			back(u, u+n);
			E[p].f = E[p^1].f = 0;
			stk[++tp] = u;
		}
	}
	sort(stk+1, stk+tp+1);
	printf("%lld %d\n", mxf, tp);
	F(i, 1, tp) printf("%d ", stk[i]);
	puts("");
}
int main() {
	scanf("%d", &T);
	while(T--) {
		init();
		solve();
	}
	return 0;
}
评测记录